Sines and Cosines on the Datatrons - Part II

Recovering the SIN() and COS() Functions

Once again, I had a chance to review the BALGOL 220 implementation of a function versus Don Knuth's implementation of the same function for Clevite Corporation in Cleveland.  This time I was hoping to find a 30 word version of the SIN() function.

I first checked out the SIN() implementation in the BALGOL compiler for the Burroughs 220.  Uh-oh, - 56 words versus the 31 words on the 205 that calculate both SIN() and COS().

 

 

However, the polynomial calculation of Sine involving powers of x only involves 5 multiplications and x raised to the 9th power in the BALGOL version versus 9 multiplications and x raised to the 17th power in the Clevite version.  

 

As with the square root subroutine discussed previously, it is worth examining the two approaches more closely.  First though, a bit of theory.

 

You might recall from calculus class that there is an infinite series that will approximate the Sine of x.  This is called a Taylor series (and in this specialized case, a MacLaurin series) and looks like this:

 

 

That looks like a series that ought to converge pretty quickly - as long as x is less than 1 (or at least not much bigger than 1) - after all, 11! is about equal to 40 million.   

Now, let's think about what value x is going to be in our calculation.  First, x will need to be an angle measured in radians, not degrees.  That is, a full 360 degrees will be represented as 2.0 Pi radians, or about 6.28  A value of 6 in that series may not lead to quick convergence.  And our x could be any value - even in the hundreds, thousands or more.

Looking at a graph, however, the cyclical nature of the sine function suggests that just covering 0 to 360 degrees will cover all possibilities.  

 

 

 

Noting that values from 180 to 360 are just the negative of 0 to 180 suggests we could cut that interval in half.  And since the upside and downside of that smaller interval are symmetrical, we can maybe get by with just calculating values for 0 to 90 degrees.  That is good news: 90 degrees is just Pi/2 in radians or around 1.57  It turns out that for values between 0 and 90 degrees, seven terms of this series will give us eight digit accuracy.  This looks like a plan!

Let's use abbreviated versions of this series to calculate the sine of 90 degrees.

 

 

 

The BALGOL SIN() subroutine for the Burroughs 220 first uses a scaling technique to reduce the original input value to a result in the interval -90 to 90 degrees. It does this with the following techniques:

1. Multiply the input by 1/Pi - effectively changing the radian input into "half cycles."  For instance, 126.44910 radians (this is 20 x 2Pi +Pi/4)  becomes 40.249999.  We throw away the digits before the decimal point and are left with 0.249999 That is one quarter of a half-cycle or 45 degrees.
   
   
2. Now, double the value.  The net effect to this point is to have multiplied by 2/Pi which converts our original input value in radians to a fraction of a quarter cycle.  If that fraction is greater than 1, we subtract 2 from it.  This always yields a decimal fraction between -1 and 1  corresponding to an angle between -90 and 90 degrees as input to the next step.
   
   
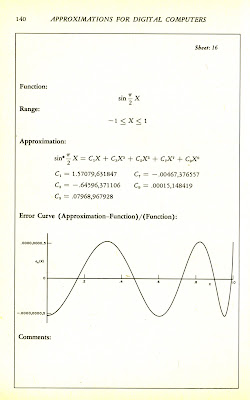
3. Use a Power series of 5 terms to calculate a Sine value.  0.70710678 in this case.
   Specifically:
   

   SIN(x) = Ax+Bx^3+Cx^5+Dx^7+Ex^9
   where
   A=   6.2831849
   B= -41.341677
   C=  81.604783
   D= -76.701934
   E=  42.040797

4. Adjust the results if the original input was a value that required the result to be negative.
   
   
5. Return to the calling program.
   

That seems straightforward.  And it is easy enough to check out those coefficients versus the ones in the Maclaurin series.  We just factor out the 2/Pi raised to the various powers.

 

 

 

Well, that's interesting.  The BALGOL coefficients are similar to the "adjusted" MacLaurin coefficients but differ by increasing amounts in the higher powers.  Perhaps this is not a MacLaurin Series.  We had better explore a bit more.  (In fact, while the five-term MacLaurin series works quite well up to 45 degrees, it breaks down badly as we approach 90 degrees.  We would need at least six terms to get 7 digit accuracy.)

Enter Cecil J. Hastings, Jr., The Great Approximator.

As was the case with the Square Root function, it helps to go back to the late 1940s and browse through some of the literature from the IBM Computation Seminar held in Endicott, NY in December of 1949.  This was the first of the conferences organized by Cuthbert Hurd after joining IBM.  IBM Customers were still in the early stages of learning to compute with the IBM 604 electronic calculating punch and the Card Programmed Calculator (CPC).

 

Cecil Hastings, Jr. of RAND Corporation contributed a paper on the approximation of various functions with calculations to replace tables on cards.  Hastings, over the next few years, would develop a library of approximations that he distributed on loose-leaf sheets to interested subscribers.  These, in effect, became the subroutine library for the 604 and CPC.

 

        

   
 

Willis Ware, in his memoir of the early RAND years notes that Bob Bemer (Mr. ASCII) actually drew some of the error curves for Hasting's charts.

 

In 1954, RAND published the approximations, with detailed error curves in the form of a book titled Approximations for Digital Computers.  Besides the approximations themselves, it included a one hundred and twenty page exposition of approximation theory and practice that had originally been given as a presentation to the Los Angeles Chapter of the Digital Computers Association in 1953. 

Hastings was dubbed "The Great Approximator" by Herb Grosch.  Lacking a PhD, he never gained the stature of other early Numerical Analysts but his work is embedded in much of the computing of the 1950s and 60s as shown here.

Well, there in chart 16 of Hasting's approximations, we have the formula, the coefficients and the error curve for the BALGOL Sine function:

 For anyone interested in pursuing the math in depth, I recommend Hasting's book, or any treatise on Chebyshev polynomial approximation.  If you want just a little more information about why this form of approximation is important, you can judge from this chart found at Math Stack Exchange.

 

  

Back to the 205 version of ALGOL 58

 

The Clevite SIN() subroutine from Don Knuth takes a different approach from the BALGOL scheme.  Rather than modifying the input angle to fit within a -90 to plus 90 degree range, Knuth found a power series that would converge adequately over a -360 to +360 degree range.  This requires a (probably) Chebyshev polynomial with nine terms.  The Clevite routine was written expecting the input to be in degrees and takes the following steps:

1. Multiply by 1/360 - effectively, effectively changing the input into "full cycles."  For instance, 7245 degrees (this is 20 x 360 +45)  becomes 20.125  We throw away the digits before the decimal point and are left with 0.125 That is one eighth of a full cycle or 45 degrees.  No further adjustments are required.
   
   
2. Use a power series of 9 terms to calculate a Sine value.  00.70710678 in this case.
   
   
3. Return to the calling program,

How well does it work?  I drew my own error curve and compared it to the BALGOL results.  The manual only promises seven digits of accuracy and the routine comes close:

Using a MacLaurin series of equal power would also work very well out to 180 degrees but then definitely goes "off the chart."  Where did the coefficients come from for the 205 version?  I don't have an answer for that.  But it is worth noting that the common method for finding a Sine or Cosine in the 1950s and 1960s, was to get out the Chemical Rubber Company's book of Standard Mathematical Tables and look them up.  

This handy publication was produced in Cleveland with the assistance of considerable labor obtained at Case Institute.  A commenter at the John Cook Blog left this description of how the labor was obtained:

1. R E Van Valkenburgh

29 November 2014 at 18:11

This also brings up the question of how the manual labor for number crunching has been acquired.

For those of you who remember the huge, “Handbook of Chemistry and Physics” (still?) published by the former Chemical Rubber Company (now CRC Press)… my dad used to tell us how the students at the then Case Institute of Technology (not Case-Western Reserve University) were conscripted to calculate the large number of large tables. Hey, it never hurt your grade if your professor asked you to volunteer.

Not only is it remarkable how some of these things were calculated; but even more remarkable how accurate they often were. (Case & the CRC had multiple independent calculations to help identify errors, according to dad.)

So there would have been plenty of expertise around the Case campus to support Sine approximations.  Still, it might have been better to limit the input to range to just 180 degrees and adjust accordingly.

Of some interest is what happens as the initial input angle grows - for example, into the thousands or more, and we discard the first several digits - what happens to our accuracy?  We could lose signifiance.  Lop off the leading three or four digits of the angle, and we are left with only five or four digits as our input.  The BALGOL manual addresses this - but only when we have an angle greater than ten million and lose all significance.  The manual and the compiler note an error message:      RESULT ILL-DEFINED FOR SIN  On the 205, you are on your own to be aware of the problem.

Calculation of the COSINE

The Cosine function is a simple addition to the subroutine library.  Since the Cosine function is equal to the Sine function offset by 90 degrees, this subroutine consists of a single addition instruction placed immediately before the Sine subroutine adding 90 degrees to the submitted angle.

 

Addendum for the Modern Era

Accuracy is not the only concern when calculating Sines and Cosines on a computer.  Speed is also an issue.  At about the same time as our two Datatron compilers were being written, a new method for calculating these functions was being developed within Convair Corporation's group working on a navigation computer for the B-58.  The method was not published for a while but apparently became very popular among calculators and computers that did not have a hardware multiplication capability.  There was a time when "multiplications per second" was a key performance measure for computers.  The new method is known as CORDIC, involves no multiplications and is worth reading about either in Wikipedia or a serious paper if you have a math and hardware inclination.  The always informative Ken Sherriff Blog has a post on CORDIC as found in the 8087 math coprocessor.  He includes photos of the coefficients hard coded into the 8087.

Is speed a concern on either the BALGOL or Clevite implementation of SIN(x)?  I don't think so;  the Clevite routine runs faster than the square root subroutine on the 205.  I will come back to the question, however, in a later blog post about benchmarking these old machines.

 

Additional Notes and Resources:

An exhaustive set of coefficients of polynomials for approximating SIN(x) carried out to 36 digits can be found under the title Fast Minimax Polynomial Approximations of Sine and Cosine; it can be found here.  See the Summary in Appendix B for development details.  This may be the best source of approximating polynomials on the Internet but I had no luck mapping them back to Knuth's set - probably because they were optimized on the interval (0, 90) rather than on (0, 360).

The original paper published in this area appears to be the Remez Exchange Algorithm published (in French) in 1934.

Numerical Methods for Scientists and Engineers, first published in 1962 by R. W. Hamming, is likely the definitive work on Approximation Theory from the early years.  Hamming, then at Bell Labs, was also a presenter at the 1949 seminar in Endicott.

Modern treatment of the subject can be found in Approximation Theory and Approximation Practice by Lloyd N. Trefethen (SIAM, 2013)